高等数学作为数学领域的一个重要分支,主要研究变量、函数、极限、导数、积分、级数、微分方程、多元函数、空间解析几何、场论等内容,这些内容不仅构成了数学分析的核心框架,还为物理学、工程学、经济学、计算机科学等多个学科提供了理论基础和解决问题的工具,以下从多个维度详细阐述高等数学的研究内容。

函数与极限
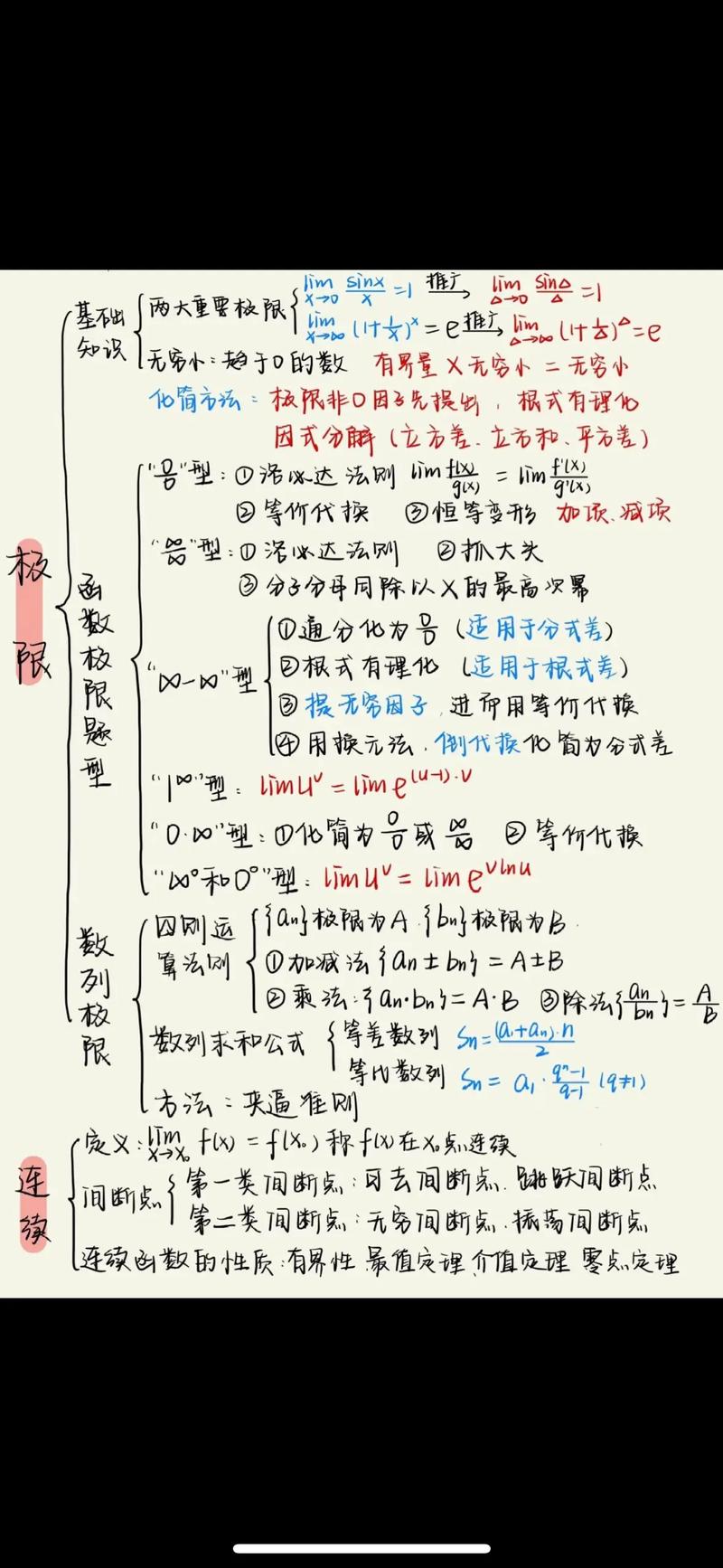
函数是高等数学的研究对象,描述了变量之间的依赖关系,高等数学首先研究函数的基本性质,如定义域、值域、单调性、奇偶性、周期性等,极限则是高等数学的基石,用于研究函数在自变量变化过程中的趋势,极限的概念包括数列极限和函数极限,通过ε-δ语言严格定义,为后续的导数、积分等概念奠定了基础,极限的研究还涉及无穷小量与无穷大量的比较、极限的运算法则、两个重要极限(lim(x→0)sinx/x=1和lim(x→∞)(1+1/x)^x=e)等内容。
一元函数微分学
微分学主要研究函数的局部变化率,导数是微分学的核心概念,表示函数在某一点处的瞬时变化率,导数的计算包括基本初等函数的导数公式、导数的四则运算法则、复合函数求导法则、隐函数求导法、参数方程求导法等,微分则描述函数在局部线性近似中的变化量,与导数密切相关,微分学的应用十分广泛,如求函数的单调区间、极值、最值,以及函数图像的绘制(通过研究凹凸性、拐点、渐近线等),中值定理(如罗尔定理、拉格朗日中值定理、柯西中值定理)是微分学的重要理论工具,用于证明不等式、分析函数性质等。
一元函数积分学
积分学是高等数学的另一核心内容,主要包括不定积分和定积分,不定积分是求导数的逆运算,研究所有原函数的集合,计算方法包括直接积分法、换元积分法、分部积分法等,定积分则表示函数曲线与坐标轴所围成的“有向面积”,其定义通过分割、近似求和、取极限的步骤严格给出,微积分基本定理(牛顿-莱布尼兹公式)揭示了微分与积分的内在联系,将定积分的计算转化为求原函数的问题,积分的应用包括求平面图形的面积、旋转体的体积、曲线的弧长,以及物理学中的功、压力、质心等问题,反常积分(无穷积分和瑕积分)拓展了积分的研究范围。
无穷级数
无穷级数是研究无限项求和的数学工具,包括常数项级数和函数项级数,常数项级数的研究重点在于其收敛性,通过比较判别法、比值判别法、根值判别法等方法判断级数是否收敛,函数项级数中,幂级数和傅里叶级数尤为重要,幂级数是形如∑a_n(x-x₀)^n的级数,具有收敛半径和收敛域,可用于表示函数和近似计算,傅里叶级数则将周期函数表示为正弦函数和余弦函数的无穷级数,在信号处理、热传导等领域有广泛应用,级数的收敛性、一致收敛性、和函数的性质等是研究的关键问题。
多元函数微分学
多元函数微分学将一元函数的推广到多个自变量的情况,偏导数描述函数沿某一坐标轴方向的变化率,全微分则刻画函数在多维空间中的线性近似,方向导数和梯度用于研究函数在任意方向的变化率,梯度方向是函数增长最快的方向,多元函数的极值问题需要通过求解偏导数为零的点(驻点),并结合黑塞矩阵判断极值性质(极大值、极小值或鞍点),多元微分学还涉及隐函数存在定理、条件极值(拉格朗日乘数法)等内容,为优化问题提供了理论基础。
多元函数积分学
多元函数积分学包括二重积分、三重积分、曲线积分和曲面积分,二重积分用于计算平面区域上的函数积分,可通过直角坐标或极坐标计算;三重积分则用于三维空间中的积分,计算方法包括直角坐标、柱坐标和球坐标,曲线积分分为对弧长的曲线积分和对坐标的曲线积分,分别用于计算曲线上的质量、功等问题,曲面积积分同样分为对面积的曲面积积分和对坐标的曲面积积分,涉及曲面的通量等物理概念,格林公式、高斯公式、斯托克斯公式是多元积分的重要公式,将不同类型的积分联系起来,简化了计算过程。
微分方程
微分方程是含有未知函数及其导数的方程,分为常微分方程和偏微分方程,常微分方程的研究包括一阶方程(如可分离变量方程、齐次方程、线性方程)和高阶方程(如线性常系数齐次和非齐次方程),解微分方程的方法包括初等积分法、拉普拉斯变换法、数值解法等,偏微分方程则研究多元函数的偏导数方程,如热传导方程、波动方程、拉普拉斯方程,是描述物理现象的重要工具,微分方程在动力学、电磁学、经济学等领域有广泛应用。
空间解析几何与场论
空间解析几何用代数方法研究空间中的几何图形,包括向量运算、空间直线与平面方程、曲面方程(如球面、柱面、锥面)等,场论研究标量场和向量场的性质,包括梯度、散度、旋度等概念,梯度用于标量场的方向导数,散度描述向量场的源强度,旋度刻画向量场的旋转程度,场论的基本定理(如梯度定理、散度定理、旋度定理)将场的局部性质与整体性质联系起来,在电磁学、流体力学等领域有重要应用。

相关问答FAQs
问题1:高等数学中的极限为什么如此重要?
解答:极限是高等数学的基石,它为导数、积分、级数等核心概念提供了严格的数学基础,导数的定义是通过函数增量与自变量增量比值的极限来描述的;定积分则是通过分割区间、求和、取极限的过程定义的,没有极限,这些概念就无法精确表述,微积分的理论体系也将无法建立,极限还用于分析函数的连续性、渐近行为等性质,是连接初等数学与高等数学的桥梁。
问题2:多元函数微分学与一元函数微分学的主要区别是什么?
解答:多元函数微分学是一元函数微分学的推广,但存在显著区别,研究对象从单变量函数扩展到多变量函数,导致导数概念分化为偏导数、全微分、方向导数等,一元函数的极值问题通过一阶导数和二阶导数即可判断,而多元函数的极值需要求解驻点并结合黑塞矩阵(二阶偏导数矩阵)分析,过程更为复杂,多元微分学中涉及隐函数存在定理、拉格朗日乘数法等独特内容,且几何意义从平面曲线上升到空间曲面或超曲面,分析维度更高,应用场景也更广泛。