数学课题研究专题小结

在本次数学课题研究过程中,我们围绕“函数图像变换与性质探究”这一主题,通过理论分析、数据验证和案例实践相结合的方式,系统研究了函数平移、伸缩、对称等变换规律及其对函数单调性、奇偶性、周期性等性质的影响,研究过程中,我们首先梳理了基本初等函数的图像特征,借助几何画板等工具动态演示变换过程,记录关键参数变化与函数性质的对应关系,并通过Excel进行数据统计与误差分析,最终归纳出具有普适性的结论。
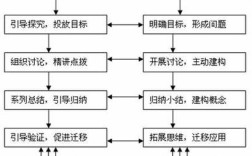
在研究方法上,我们采用了“问题驱动—实验探究—理论验证—模型构建”的四步法,在探究函数y=f(x+a)的平移规律时,我们选取y=x²、y=sinx等典型函数,通过改变参数a的值(如a=1,2,-1等),观察图像左右平移的距离与方向,发现当a>0时图像向左平移a个单位,a<0时向右平移|a|个单位,并通过定义域、值域的变化验证了这一结论的正确性,对于复合函数的变换,如y=Asin(ωx+φ),我们重点分析了A、ω、φ三个参数对振幅、周期、相位的影响,通过控制变量法设计实验,记录不同参数组合下函数图像的形态特征,总结出“振幅由A决定,周期T=2π/|ω|,相位平移由φ/ω共同决定”的规律。
在数据收集与处理阶段,我们建立了参数变化与函数性质对应关系的数据库,部分关键数据如下表所示:
| 函数类型 | 参数变化 | 图像变换特征 | 性质影响 |
|---|---|---|---|
| y=f(x)+b | b>0 | 向上平移b个单位 | 值域整体上移b个单位 |
| y=af(x) | a>1 | 纵向伸长为a倍 | 值域范围扩大a倍 |
| y=f(-x) | 关于y轴对称 | 奇偶性改变(偶变奇) | |
| y=f( | x |
研究过程中,我们也遇到了一些问题,在探究分段函数的变换规律时,由于分段点的位置变化导致图像出现“断点”,初期难以准确描述变换后的函数表达式,通过查阅资料和小组讨论,我们采用“分段点优先法”,先确定变换后分段点的坐标,再分别求解各段函数的解析式,最终解决了这一问题,对于抽象函数(如y=f(x)+f(-x)),由于缺乏具体图像支撑,我们通过构造特殊函数(如指数函数、对数函数)进行类比分析,逐步归纳出其奇偶性特征。

通过本次研究,我们不仅深化了对函数变换理论的理解,还提升了数学建模与实验探究能力,我们发现,函数变换的本质是“坐标变换”,即通过改变自变量或因变量的映射规则,实现对图像的平移、伸缩或对称操作,这一结论不仅适用于初等函数,也可推广至更一般的函数空间,研究也揭示了数形结合思想的重要性——许多抽象的代数性质可以通过直观的图像特征展现,反之亦然。
本次研究仍存在局限性,仅研究了连续函数的变换,未涉及离散函数或随机函数;对于多参数复合函数的变换,未能建立统一的量化模型,未来可进一步拓展研究范围,引入矩阵变换等高等数学工具,探索函数变换在非线性动力系统中的应用。
本次数学课题研究不仅巩固了课堂所学知识,更培养了科学探究精神与合作能力,通过亲身实践,我们深刻体会到数学不仅是抽象的符号体系,更是描述现实世界的有力工具,在今后的学习中,我们将继续秉持“观察—猜想—验证—推广”的研究思路,不断探索数学的奥秘。
相关问答FAQs
Q1:函数图像变换中,参数的正负如何影响平移方向?
A1:在函数y=f(x+a)中,参数a的正负决定平移方向,当a>0时,图像向左平移a个单位;当a<0时,图像向右平移|a|个单位,y=f(x+2)是将y=f(x)向左平移2个单位,而y=f(x-3)则是向右平移3个单位,这一规律源于函数定义域的调整:x+a相当于将自变量x替换为x+a,导致图像沿x轴反向移动。
Q2:如何判断函数变换后的奇偶性是否改变?
A2:函数变换后的奇偶性取决于变换是否改变对称性,y=f(-x)会将原函数关于y轴对称,若原函数为奇函数(f(-x)=-f(x)),则变换后变为偶函数(f(-x)=-f(x)→y=f(-x)=-f(x),但新函数g(x)=f(-x)满足g(-x)=f(x),若f(x)为奇函数,则g(-x)=-f(-x)=g(x),故为偶函数),而y=f(x)+a(a≠0)会破坏奇偶性,因为g(-x)=f(-x)+a,若f(x)为奇函数,则g(-x)=-f(x)+a≠±g(x),除非a=0,平移变换(非零)会改变奇偶性,而对称变换(如y=f(-x))可能改变奇偶性类型。