微积分的发展史是一部融合了数学思想、物理需求和技术进步的宏大史诗,其演变过程跨越了数个世纪,从早期的萌芽思想到严格的公理化体系,再到现代的广泛应用,深刻影响了科学和工程领域的发展,以下将从关键时期、核心人物及贡献、重要文献等方面,系统梳理微积分的发展脉络,并辅以表格总结关键节点,最后以FAQs形式解答常见疑问。

微积分的萌芽时期(17世纪前)
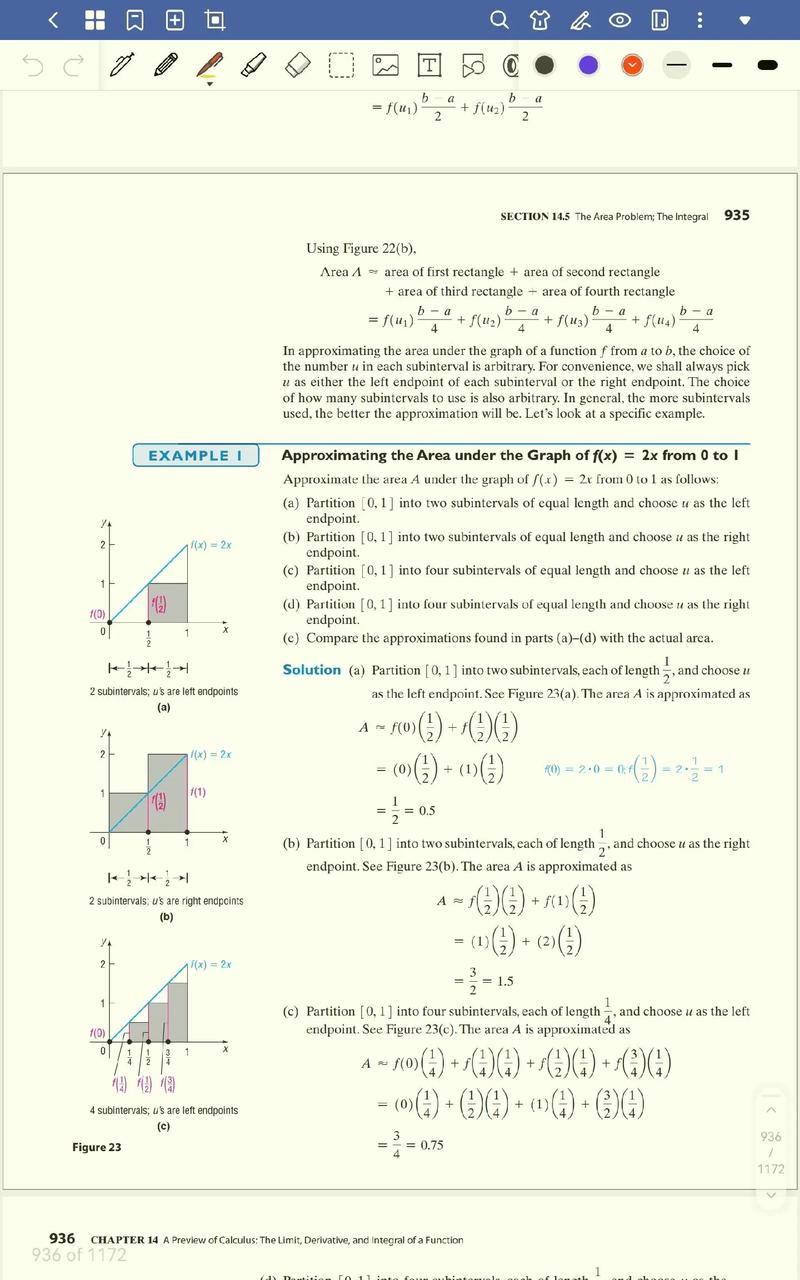
微积分的思想雏形可追溯至古代文明,古希腊的阿基米德在《论球与圆柱》中通过“穷竭法”计算了球体和抛物线弓形的面积,这种方法蕴含了极限的思想,被视为积分学的早期萌芽,中国战国时期的《庄子·天下》篇中“一尺之棰,日取其半,万世不竭”也体现了极限的朴素观念,古代数学缺乏系统的符号和逻辑框架,这些思想未能形成完整的理论体系。
到了中世纪,印度和阿拉伯数学家对无穷小量有了进一步探索,12世纪的印度数学家婆什迦罗二世在计算圆面积时使用了类似极限的方法,而14世纪的法国数学家奥雷姆通过“形态幅度理论”研究了变化率问题,这些工作为微积分的出现奠定了基础。
微积分的创立时期(17世纪)
17世纪是微积分诞生的关键时期,随着欧洲科学革命的兴起,物理学家和数学家对运动、变化和连续量的研究需求激增,直接推动了微积分的创立。
- 牛顿的贡献:艾萨克·牛顿从物理学问题出发,发展了“流数术”(Method of Fluxions),他在1666年的《流数短论》中提出,变量是连续运动的点,其导数(流数)是运动的速度,积分则是原函数(流量),牛顿将微积分应用于解决天体运动、力学等问题,如万有引力定律的推导,但他的工作以几何形式呈现,直到1687年《自然哲学的数学原理》中才部分公开。
- 莱布尼茨的贡献:戈特弗里德·莱布尼茨从几何问题出发,独立发展了微积分的符号体系,他在1684年发表《一种求极大值与极小值和切线的新方法》,首次引入了dx、dy等符号,并系统阐述了微分和积分的基本法则,莱布尼茨的符号更直观且便于运算,至今仍被广泛使用。
- 优先权之争:牛顿与莱布尼茨关于微积分发明权的争论持续多年,现代研究认为两人是独立完成的,但莱布尼茨的符号体系对微积分的传播起到了关键作用。
微积分的发展与严格化(18-19世纪)
18世纪,微积分被广泛应用于物理和工程领域,欧拉、拉格朗日等数学家通过推广函数概念、发展变分法等,扩展了微积分的应用范围,由于缺乏严格的逻辑基础,微积分中“无穷小量”的模糊性引发了争议,如贝克莱主教在《分析学家》中批评无穷小量是“逝去量的鬼魂”。

19世纪,数学家开始为微积分构建严格的理论基础。
- 柯西的贡献:奥古斯丁-路易·柯西在《分析教程》(1821)中首次用极限概念定义了连续、导数和积分,消除了无穷小量的模糊性。
- 魏尔斯特拉斯的贡献:卡尔·魏尔斯特拉斯通过ε-δ语言严格化了极限理论,彻底解决了微积分的逻辑问题,使分析学走向严格化。
- 黎曼与勒贝格的贡献:伯恩哈德·黎曼发展了黎曼积分理论,亨利·勒贝格则进一步创立勒贝格积分,扩展了积分的应用范围。
微积分的现代发展与拓展(20世纪至今)
20世纪以来,微积分与其他数学分支深度融合,发展出实分析、复分析、泛函分析等学科,并在计算机科学、经济学、生物学等领域得到广泛应用,微分方程成为描述动态系统的核心工具,而数值分析则为微积分的计算机实现提供了方法。
关键人物与文献总结表
| 时期 | 关键人物 | 主要贡献 | 代表性文献 |
|---|---|---|---|
| 古代 | 阿基米德 | 穷竭法计算面积,极限思想萌芽 | 《论球与圆柱》 |
| 中世纪 | 奥雷姆 | 形态幅度理论,研究变化率 | 《论均匀与非均匀的强度》 |
| 17世纪 | 牛顿 | 流数术,应用于物理学 | 《自然哲学的数学原理》(1687) |
| 17世纪 | 莱布尼茨 | 微分积分符号系统,微积分基本法则 | 《一种求极大值与极小值和切线的新方法》(1684) |
| 19世纪 | 柯西 | 极限理论严格化,定义连续、导数、积分 | 《分析教程》(1821) |
| 19世纪 | 魏尔斯特拉斯 | ε-δ语言,严格化极限理论 | 《论 analytic 函数》(1874) |
| 19世纪末 | 黎曼 | 黎曼积分理论 | 《关于利用三角级数表示一个函数的可能性》(1854) |
| 20世纪 | 勒贝格 | 勒贝格积分,扩展积分范围 | 《积分、长度与面积》(1902) |
相关问答FAQs
Q1:为什么牛顿和莱布尼茨的微积分发明会引发争议?
A1:牛顿与莱布尼茨的争议主要源于发明时间的先后和表述方式的差异,牛顿在1660年代已发展流数术,但直到1687年才发表部分成果;莱布尼茨在1670年代独立研究,并于1684年率先发表微分论文,两人使用的符号体系不同(牛顿用点表示导数,莱布尼茨用dx/dy),且早期通信中曾交换过思想,导致双方支持者指责对方抄袭,现代数学史研究表明,两人是独立完成的,但莱布尼茨的符号体系更便于推广,因此微积分的基本法则通常以莱布尼茨命名。
Q2:微积分的严格化对数学发展有何意义?
A2:微积分的严格化解决了早期理论中“无穷小量”的模糊性问题,使数学分析从直观的几何描述转向逻辑严密的公理化体系,柯西的极限理论和魏尔斯特拉斯的ε-δ语言不仅巩固了微积分的基础,还推动了实分析、复分析等学科的发展,为20世纪现代数学的严谨性奠定了基础,严格化后的微积分避免了逻辑矛盾,使其在物理学、工程学等领域的应用更加可靠,同时也促进了数学与其他学科的深度融合。