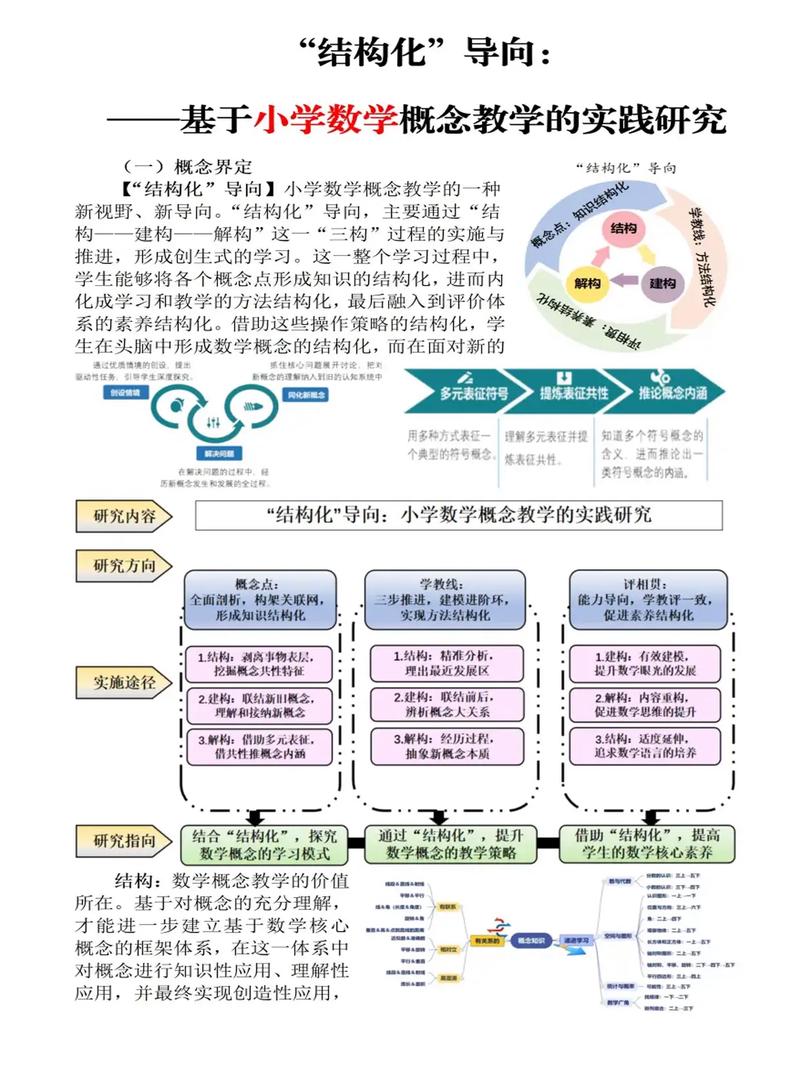
数学概念教学研究重点一直是教育领域的核心议题,其核心在于帮助学生构建准确、深刻且可灵活运用的数学认知结构,这一研究涉及多个维度,从概念的抽象本质到学生的认知规律,再到教学方法的创新与实践,需要系统性地展开分析。

数学概念的内涵与外延界定是研究的基础,数学概念具有高度的抽象性和逻辑性,它是对现实世界数量关系和空间形式的本质概括。“函数”这一概念,其内涵是“两个非空数集之间的对应关系,且一个自变量唯一确定一个因变量”,而其外延则包括一次函数、二次函数、指数函数、三角函数等所有满足此定义的具体函数,在教学研究中,必须明确区分概念的本质属性与非本质属性,避免学生形成片面或错误的认知,本质属性是决定概念核心特征的要素,如函数中的“单值对应”;非本质属性则是概念在具体表现中的多样性,如函数解析式的形式、图像的形状等,教师需要通过正例、反例的辨析,帮助学生抓住概念的本质,通过展示y=x²和y=²x(后者在实数范围内不构成函数)的对比,强化学生对“单值对应”这一本质属性的理解,概念之间的逻辑关系,如属种关系(如“矩形”与“正方形”)、并列关系(如“加法”与“乘法”)和交叉关系等,也是内涵与外延研究的重要内容,这有助于学生构建系统化的知识网络。
学生数学概念的形成机制与认知障碍是研究的重点方向,根据皮亚杰的认知发展理论,学生数学概念的形成是一个从具体到抽象、从感性到理性的主动建构过程,在这一过程中,学生的已有认知经验(即“前概念”)扮演着双重角色,合理的生活经验可以成为概念学习的“脚手架”,如用“分蛋糕”理解分数;一些朴素、直觉的观念也可能成为认知障碍,如认为“0不是自然数”或“角的大小与边的长度有关”,教学研究需要深入分析不同年龄段学生的思维特点,识别其概念学习的“关键节点”和“典型误区”,小学生对“平均数”的理解往往停留在“移多补少”的层面,难以把握其“刻画数据集中趋势”的统计意义,初中生在学习“有理数”时,容易受算术数思维的影响,对负数的意义和运算规则感到困惑,研究需要关注如何创设有效的认知冲突情境,引发学生的思维碰撞,促使他们主动调整和重构自己的认知结构,通过“一组学生的身高数据”引入平均数,让学生感受其在不同情境下的应用,从而超越“纯粹计算”的层面。
数学概念的教学策略与模式创新是提升教学效果的关键,传统的概念教学往往采用“定义-例题-练习”的灌输式模式,忽视了学生的主体性和概念的生成过程,现代教学研究强调概念的形成应是一个“再创造”的过程,教师应引导学生经历“具体实例-抽象共性-符号表征-应用拓展”的完整认知路径,在这一过程中,多元表征策略的运用尤为重要,数学概念可以通过实物操作、图像直观、语言描述、符号公式等多种方式进行表征,这些表征之间的相互转换与联系是深化概念理解的有效途径,在“图形的旋转”概念教学中,可以通过旋转实物模型(操作表征)、观察旋转动画(图像表征)、描述旋转要素(如旋转中心、方向、角度)(语言表征)、写出旋转坐标变换公式(符号表征)等方式,帮助学生从不同角度把握概念的本质,情境化教学、问题驱动教学、合作探究教学等模式也被广泛应用于概念教学中,这些模式强调将概念置于真实或拟真实的情境中,通过解决具有一定挑战性的问题,激发学生的学习兴趣和探究欲望,使概念学习成为有意义的活动,在“概率”概念教学中,可以设计“摸球游戏”“天气预报”等情境,让学生在亲身体验中感受随机性与必然性,理解概率的意义。
数学概念的理解水平评估与教学反思是保障教学质量的重要环节,准确评估学生对数学概念的掌握程度,是调整教学策略、改进教学方法的前提,传统的纸笔测试往往侧重于概念记忆和简单应用,难以全面反映学生的深层理解,研究需要探索多元化的评估方式,如概念图绘制、访谈法、开放式问题、表现性任务等,让学生绘制“三角形”概念图,可以清晰地展示他们对三角形分类、性质等概念之间关系的理解程度,教学反思则要求教师基于评估结果和教学实践,持续审视概念教学的有效性,反思概念引入的情境是否恰当、概念的辨析是否充分、学生的认知障碍是否得到有效突破等,通过行动研究等方法,教师可以将教学实践与研究紧密结合,不断提升自身的专业素养和概念教学能力。
为了更直观地展示数学概念教学的关键策略及其应用,以下表格进行了简要概括:
| 教学策略 | 核心要点 | 应用举例(以“平行四边形”概念为例) |
|---|---|---|
| 多元表征 | 结合操作、图像、语言、符号等多种表征方式,促进概念间的联系。 | 用木条拼摆平行四边形(操作),观察其对边和对角(图像),描述“对边平行且相等”的特征(语言),写出定义符号表达式(符号)。 |
| 情境化教学 | 创设与学生生活经验相关的真实或拟真实情境,激发学习兴趣。 | 设计“学校花坛设计”情境,需要计算平行四边形花坛的面积,引入对平行四边形性质的实际需求。 |
| 概念辨析 | 通过正例、反例、变式,突出概念的本质属性,消除非本质属性的干扰。 | 展示标准的平行四边形、矩形(特殊的平行四边形)、梯形(反例)、不规则四边形(变式),引导学生辨析“对边平行”这一核心特征。 |
| 认知冲突 | 设置与学生原有认知相矛盾的问题,引发思考,促进概念重构。 | 学生可能认为“对边相等的四边形就是平行四边形”,可通过展示“等腰梯形”反例,引发认知冲突,深化对“对边平行”本质的理解。 |
相关问答FAQs:
问题1:在数学概念教学中,如何帮助学生克服“负迁移”现象,即已有知识对新概念学习的干扰?
解答:“负迁移”是概念学习中的常见障碍,如受整数减法“越减越小”的影响,学生难以理解“5-(-3)=8”这样的运算,克服负迁移需要:第一,充分暴露学生的前概念,通过课前访谈、诊断性测试等方式了解其已有认知,找准潜在的干扰点;第二,进行精准对比辨析,将新旧概念中易混淆的属性进行对比,明确其相同点与不同点,如将整数减法与有理数减法的法则、算理进行对比分析;第三,设计针对性的变式练习,通过反例、特殊案例等,强化对新概念本质属性的理解,削弱旧概念的干扰;第四,注重概念间的联系与区别,帮助学生构建清晰的知识网络,明确每个概念的适用范围和条件,如强调负数引入后,运算规则和结果的扩展性。
问题2:如何平衡数学概念的严谨性与学生认知发展阶段之间的关系,避免过度抽象导致学生理解困难?
解答:平衡概念的严谨性与认知发展阶段是概念教学的艺术,要“深入浅出”,教师自身需对概念的来龙去脉、逻辑结构有深刻理解,能用学生可接受的语言和方式进行解释,对小学生讲“圆”,不必立即给出严格的点集定义,而是通过“圆一中同长也”(《墨经》)的直观描述,结合画圆操作,让其感受圆的特征,要“循序渐进”,遵循学生的认知规律,采用“螺旋式上升”的方式呈现概念,同一概念在不同学段应有不同的要求和侧重点,如“方程”概念,小学阶段强调“含有未知数的等式”,侧重于识别和简单求解;初中阶段则强调“刻画等量关系的模型”,侧重于建模思想和一般解法,要“直观先行”,充分利用实物、模型、图像、多媒体等直观手段,帮助学生积累丰富的感性经验,为抽象概念的形成奠定基础,要“适时抽象”,当学生具备足够的感性经验后,应及时引导他们进行抽象概括,用精确的数学语言和符号表达概念,实现从具体到抽象的跨越,确保概念的严谨性。