高中函数研究论文范文

函数是高中数学的核心内容之一,贯穿于整个数学学习过程,不仅是后续高等数学的基础,也是解决实际问题的重要工具,本文以高中函数为研究对象,从函数的概念、性质、应用及教学策略等方面展开分析,旨在深化对函数的理解,提升数学思维能力。
函数的概念与表示
函数是描述两个非空数集之间对应关系的数学概念,其核心在于“对应法则”与“定义域”,在高中阶段,函数的表示方法主要包括解析式、图像法、列表法,二次函数 ( f(x) = ax^2 + bx + c )(( a \neq 0 ))通过解析式体现其对称性、单调性等性质,而通过图像法则能直观展示其抛物线特征,教学中需强调定义域的重要性,避免因忽略定义域导致的错误,函数 ( f(x) = \sqrt{x-1} ) 的定义域为 ( [1, +\infty) ),这一限制直接影响函数的取值范围和图像绘制。
函数的性质与应用
函数的性质包括单调性、奇偶性、周期性等,这些性质是解决函数问题的关键,以单调性为例,通过导数判断函数增减性是高中数学的重点,函数 ( f(x) = x^3 - 3x ) 的导数为 ( f'(x) = 3x^2 - 3 ),通过解不等式 ( f'(x) > 0 ) 可得其单调递增区间为 ( (-\infty, -1) ) 和 ( (1, +\infty) ),函数在生活中的应用广泛,如增长率模型、最优化问题等,商家利用二次函数的最小值原理计算利润最大化时的产量,体现了函数的实际价值。
函数的教学策略
函数教学应注重概念的形成过程,结合生活实例激发学生兴趣,通过温度随时间变化的曲线引入函数图像,或用手机套餐费用与通话时长的关系解释分段函数,数形结合是函数教学的重要方法,利用几何画板等工具动态展示函数图像的变化,帮助学生理解抽象概念,分层教学因材施教,针对基础薄弱的学生强化基础练习,对学有余力的学生拓展探究性问题,如函数与方程的关系、函数零点的存在性定理等。

函数与其他知识的联系
函数与方程、不等式、导数等知识紧密联系,函数零点问题本质上是方程 ( f(x) = 0 ) 的解的问题,可通过零点存在性定理判断解的存在性,导数则是研究函数性质的工具,如利用导数求函数的极值、最值,函数思想在解析几何、概率统计中也有体现,如随机变量的概率分布函数。
案例分析:二次函数的教学设计
以二次函数为例,教学设计可分为以下步骤:
- 情境导入:通过喷泉水流轨迹引出抛物线模型,建立二次函数的直观认识。
- 概念深化:通过列表、描点、连线绘制图像,总结开口方向、对称轴、顶点等性质。
- 应用拓展:解决实际问题,如“已知抛物线 ( y = ax^2 + bx + c ) 过三点,求解析式”。
- 分层练习:基础题巩固图像性质,提升题探究参数对函数的影响,挑战题解决最值问题。
以下为二次函数性质总结表:
| 性质 | 解析式特征 | 图像特征 |
|---|---|---|
| 开口方向 | ( a > 0 ) 向上,( a < 0 ) 向下 | 抛物线开口向上或向下 |
| 对称轴 | ( x = -\frac{b}{2a} ) | 直线 ( x = h ) |
| 顶点坐标 | ( \left( -\frac{b}{2a}, \frac{4ac-b^2}{4a} \right) ) | 抛物线最低点或最高点 |
| 单调性 | ( a > 0 ):对称轴左侧递减,右侧递增;( a < 0 ) 相反 | 图像上升或下降趋势 |
FAQs
Q1:如何判断函数的单调性?
A1:判断函数单调性可通过以下方法:
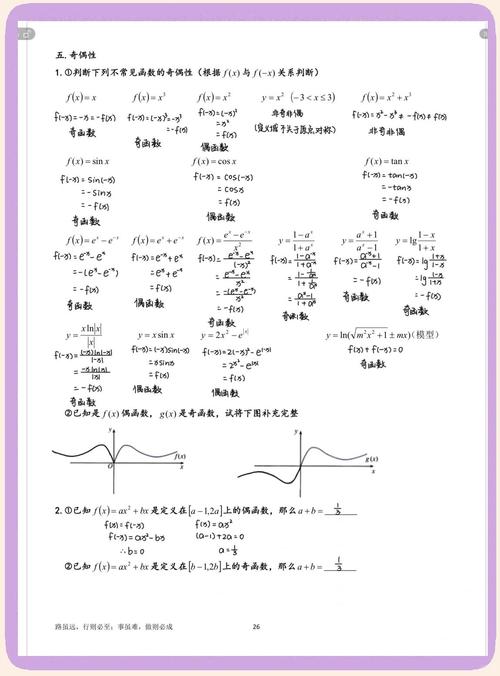
- 定义法:取区间内任意 ( x_1 < x_2 ),比较 ( f(x_1) ) 与 ( f(x_2) ) 的大小;
- 导数法:求导 ( f'(x) ),若 ( f'(x) > 0 ) 则单调递增,( f'(x) < 0 ) 则单调递减。
Q2:函数零点与方程根的关系是什么?
A2:函数零点是指函数图像与x轴交点的横坐标,即方程 ( f(x) = 0 ) 的实数根,零点存在性定理指出,若函数 ( f(x) ) 在区间 ([a, b]) 上连续,且 ( f(a) \cdot f(b) < 0 ),则该区间内至少存在一个零点。