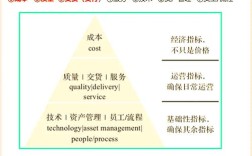
统计学及其思想是一门通过收集、整理、分析和解释数据来揭示事物规律、支持决策的科学,其核心在于从不确定性中寻找确定性,用数据说话,统计学思想贯穿于数据处理的每个环节,强调“用样本推断总体”“量化不确定性”和“控制误差”,为自然科学、社会科学、医学、经济学等领域提供了方法论基础。

统计学的基本思想可概括为“从数据中提取信息,由特殊到一般”。描述统计是基础,通过集中趋势(如均值、中位数)和离散程度(如方差、标准差)刻画数据特征,用图表(如直方图、箱线图)直观展示分布规律,某班级学生成绩的均值和标准差能反映整体水平与个体差异。推断统计是核心,基于样本数据对总体进行估计(如置信区间)和假设检验(如t检验、卡方检验),解决“小样本推断大总体”的问题,通过抽样调查估计某地区居民的平均收入,并给出误差范围。概率论是统计学的数学基础,为量化随机现象提供工具,如贝叶斯思想通过先验概率和似然函数更新后验概率,广泛应用于机器学习、医学诊断等领域。
统计学思想强调“数据背后的故事”,而非单纯计算。相关性不等于因果性是重要警示:吸烟与肺癌相关,但需通过实验设计(如随机对照试验)才能确认因果关系;模型选择需权衡偏差与方差,过于复杂的模型可能导致过拟合,而过于简单的模型则可能欠拟合,交叉验证等方法可帮助优化模型。统计思维的核心是批判性,需警惕数据采集的偏差(如样本选择偏差)、误用统计方法(如混淆p值与效应大小)或过度解读结果(如将统计显著性等同于实际重要性)。
统计学的发展离不开经典文献的支撑,C.R. Rao的《线性统计推断及其应用》系统阐述了参数估计与假设检验的理论框架;Fisher的《实验设计》奠定了实验统计的基础,提出随机化、重复性和局部控制三大原则;David Freedman的《统计学》以案例为导向,强调统计思想在现实中的应用;而《贝叶斯统计推断》则推动了现代统计与概率的融合,尤其在高维数据分析中发挥重要作用,这些文献不仅构建了统计学的理论体系,更传递了“数据驱动决策”的科学精神。
相关问答FAQs
Q1:统计学中的“显著性水平”是什么?如何选择?
A:显著性水平(α)是假设检验中预先设定的概率阈值,用于判断是否拒绝原假设(通常取0.05或0.01),选择α需权衡两类错误:α增大时,Ⅰ类错误(弃真)风险增加,Ⅱ类错误(取伪)风险降低;反之亦然,医学检验中,若假阳性后果严重(如误诊癌症),α应取较小值(如0.01);而探索性研究可适当放宽α(如0.1)。

Q2:大数据时代,传统统计学思想是否过时?
A:未过时,但需拓展,传统统计学强调小样本推断,而大数据具有海量、高维、实时等特点,需结合计算统计学(如分布式算法)和机器学习方法(如随机森林、深度学习),统计学的核心思想——如控制误差、理解不确定性、避免虚假关联——仍是大数据分析的基石,在推荐系统中,需通过A/B测试验证算法效果,这正是统计实验设计的应用。