下面我将从核心思想、通用建模框架、常用模型、完整案例以及挑战与注意事项五个方面,系统地阐述如何进行“对影响的研究”。
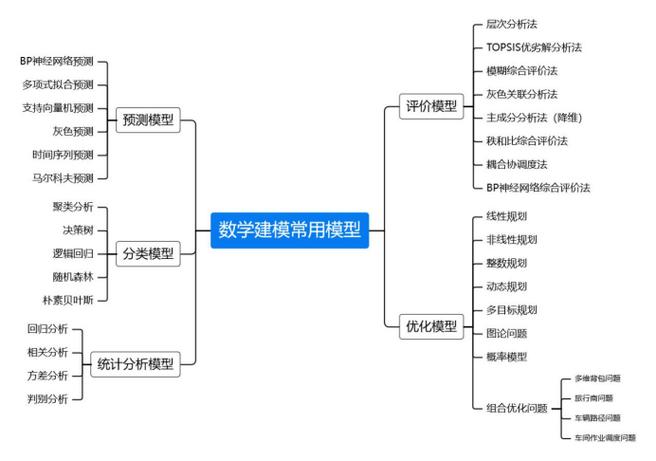
核心思想:从现实世界到数学世界
“对影响的研究”本质上是回答一个或多个问题:
- A因素对B因素有多大影响? (影响程度/强度)
- A因素如何影响B因素? (影响方式/关系,如线性、非线性、正负相关)
- 当A因素改变时,B因素会如何变化? (预测)
- 哪些因素对B的影响最大? (重要性排序)
这个过程遵循数学建模的基本流程:
- 问题抽象:将现实世界中的“影响”问题,转化为一个数学可描述的问题。
- 模型假设:明确变量,并做出必要的简化假设(如线性关系、独立性等)。
- 模型构建:选择合适的数学工具(方程、函数、算法)来描述变量间的关系。
- 模型求解:利用数据计算模型中的未知参数。
- 模型检验:评估模型的准确性、可靠性和有效性。
- 模型应用:利用模型进行预测、分析或提出决策建议。
通用建模框架(四步法)
无论具体问题是什么,研究“影响”通常可以遵循以下四个步骤:
第1步:定义问题与变量
这是最关键的一步,你需要清晰地界定:
- 因变量:你想要研究其变化的“结果”,通常是连续变量(如销售额、温度、股价)或离散变量(如是否患病、是否购买)。
- 例子:公司年销售额、城市空气质量指数、学生考试成绩。
- 自变量:你认为可能对其产生“影响”的“因素”,可以是:
- 数值型变量:广告投入(万元)、温度(℃)、学习时间(小时)。
- 类别型变量:广告类型(电视/网络)、地区(东部/西部)、教学方法(A/B)。
- 控制变量:需要保持不变或同时考虑的其他混杂因素,以避免混淆因果。
- 例子:研究广告对销售额的影响时,产品价格、竞争对手活动、季节因素等都应作为控制变量。
第2步:选择合适的模型
根据变量类型和研究目标,选择不同的模型。
| 研究目标 | 因变量类型 | 自变量类型 | 常用模型 |
|---|---|---|---|
| 预测数值 | 连续型 | 数值型、类别型 | 线性回归、多项式回归、岭回归/lasso回归 |
| 预测分类 | 离散型(0/1,是/否) | 数值型、类别型 | 逻辑回归 |
| 预测计数 | 计数型(0, 1, 2...) | 数值型、类别型 | 泊松回归、负二项回归 |
| 复杂非线性关系 | 连续型或离散型 | 数值型、类别型 | 决策树、随机森林、支持向量机、神经网络 |
| 时间序列影响 | 连续型(随时间变化) | 时间、滞后变量 | ARIMA模型、Prophet、LSTM |
第3步:模型训练与评估
- 训练:使用历史数据(训练集)来“教会”模型参数,在回归模型中,就是求解回归系数。
- 评估:使用新的数据(测试集)来检验模型的预测能力。
- 回归模型:常用指标有 R-squared (R²)、均方根误差、平均绝对误差。
- 分类模型:常用指标有准确率、精确率、召回率、F1分数、AUC值。
第4步:解释结果与应用
模型的最终目的是解释现实。
- 解读系数:在回归模型中,系数的大小和正负直接代表了影响的方向和强度,广告投入的系数为
+2.5,意味着广告投入每增加1万元,销售额预计增加2.5万元(假设其他因素不变)。 - 特征重要性:在树模型中,可以得出哪个自变量对预测结果贡献最大。
- 提出策略:基于模型结果,制定决策,如果发现网络广告的ROI(投资回报率)远高于电视广告,则建议将预算向网络广告倾斜。
常用模型详解(附适用场景)
线性回归
- 适用场景:研究多个数值型自变量对一个连续型因变量的线性影响。
- 核心公式:
Y = β₀ + β₁X₁ + β₂X₂ + ... + εY:因变量(如销售额)X₁, X₂...:自变量(如广告费、员工数)- 回归系数,直接量化了X对Y的影响,为正,表示X₁每增加一个单位,Y平均增加个单位。
- 截距
- 随机误差
- 优势:简单、可解释性强,系数具有明确的统计意义。
- 局限:假设变量间是线性关系,对异常值敏感。
逻辑回归
- 适用场景:研究多个自变量对一个二元因变量(是/否,成功/失败)的影响。
- 核心思想:它不直接预测Y,而是预测Y=1的概率,通过Logit函数将线性组合映射到(0, 1)区间。
- 核心公式:
P(Y=1) = 1 / (1 + e^-(β₀ + β₁X₁ + ...)) - 解读系数:系数 的指数
e^β₁是优势比,OR=1.5意味着,自变量X₁每增加一个单位,事件发生的“优势”(Odds)变为原来的1.5倍。
决策树 / 随机森林
- 适用场景:当变量间关系复杂、非线性,或同时存在数值型和类别型变量时,用于预测和特征重要性分析。
- 核心思想:
- 决策树:通过一系列“是/否”问题将数据分割,直到得到最终的预测结果,分割的依据是使每个节点内的数据“纯度”最高。
- 随机森林:构建大量的决策树,并取它们的平均值(回归)或投票结果(分类),以提高准确性和稳定性。
- 解读影响:
- 特征重要性:模型会输出一个列表,显示哪个变量在分割数据时被使用得最多,从而对结果影响最大。
- 可视化:决策树本身就是一个清晰的决策流程图,展示了不同变量如何相互作用并影响最终结果。
完整案例:研究“广告投入对销售额的影响”
问题定义
- 目标:量化不同广告渠道(电视、网络)的投入对公司月度销售额的影响。
- 因变量:月度销售额(万元,连续型)。
- 自变量:
- 电视广告投入(万元,数值型)
- 网络广告投入(万元,数值型)
- 控制变量:
- 促销活动次数(数值型)
- 季节因素(类别型:Q1, Q2, Q3, Q4)
模型选择
因变量是连续型,自变量包含数值型和类别型,目标是量化影响。多元线性回归是首选模型。
模型构建与求解
假设我们收集了12个月的数据,并使用统计软件(如Python的statsmodels库)进行回归分析,得到以下结果:
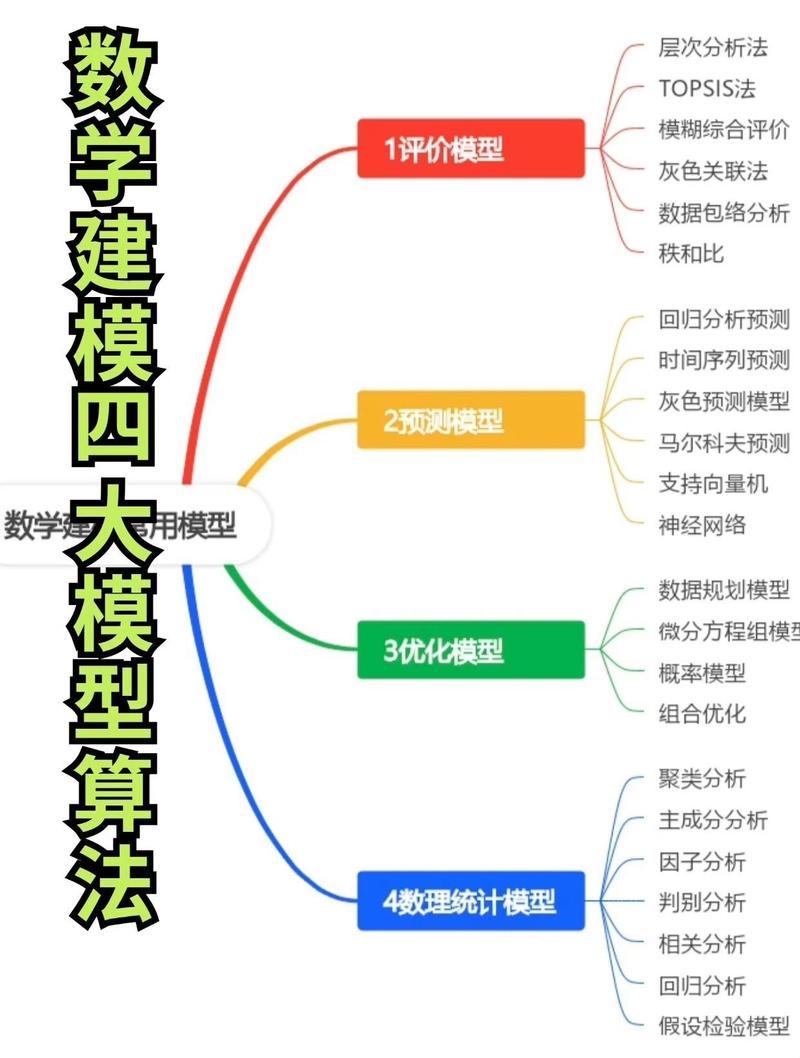
| 变量 | 回归系数 | P值 |
|---|---|---|
| 截距 | 0 | 01 |
| 电视广告投入 | 2 | 05 |
| 网络广告投入 | 5 | 001 |
| 促销活动次数 | 0 | 02 |
| 季节(Q2 vs Q1) | 0 | 1 |
| 季节(Q3 vs Q1) | 0 | 05 |
| 季节(Q4 vs Q1) | 0 | 001 |
结果解释与应用
- 系数解读:
- 网络广告投入的系数为3.5,且P值极低(0.001),说明它对销售额有显著的正向影响,在控制其他因素不变的情况下,网络广告每投入1万元,销售额预计增加3.5万元。
- 电视广告投入的系数为1.2,P值为0.05,说明它也有正向影响,但影响力显著小于网络广告,每投入1万元,销售额预计增加1.2万元。
- 促销活动也有显著正面影响。
- 季节因素:Q4(年底)的销售额比Q1(年初)高出25万元,说明年底是销售旺季。
- 应用建议:
- 预算倾斜:应优先增加网络广告的预算,其投资回报率最高。
- 组合策略:结合促销活动和旺季效应,在Q4加大广告和促销投入,可以最大化销售额。
- 进一步研究:可以研究网络广告投入是否存在“边际效应递减”现象,即当投入超过某个阈值后,其影响力是否会下降,这需要引入多项式回归。
挑战与注意事项
- 相关不等于因果:这是研究影响时最大的陷阱,模型只能揭示变量间的统计相关性,无法直接证明因果关系,冰淇淋销量和溺水人数高度相关,但并非冰淇淋导致溺水,而是“高温”这个共同原因导致了两者上升,需要通过严谨的实验设计(如A/B测试)或因果推断模型来辅助判断。
- 多重共线性:在回归中,如果自变量之间高度相关(如广告总预算和网络广告预算),模型将难以区分它们各自独立的影响,这会导致系数估计不稳定,可以通过计算方差膨胀因子来检测,并通过岭回归或删除变量来解决。
- 模型过拟合/欠拟合:模型过于复杂(如高阶多项式或深度过大的决策树)会完美拟合训练数据,但对新数据泛化能力差(过拟合),模型过于简单则无法捕捉数据中的规律(欠拟合),需要通过交叉验证等方法来选择最佳模型。
- 数据质量:模型的优劣极大依赖于数据,数据量不足、存在大量缺失值或异常值,都会严重影响结果的可靠性。
在数学建模中研究“影响”,是一个系统性的过程,它将现实问题抽象为数学语言,通过选择和构建模型来量化变量间的关系,其核心在于清晰的变量定义、合适的模型选择、严谨的统计检验和结合现实的合理解读,从经典的线性回归到现代的机器学习模型,为不同复杂程度的问题提供了丰富的工具,帮助我们更深刻地理解和改造世界。